Having fun with science and technology.
The Quantum Machine that Both Works and Doesn't
2007-08-22
As some of you may know, I wrote my diploma thesis on transport in quantum thermodynamics. Related to this work, we now put up a paper on arXiv, describing how to incorporate the concepts of work and heat, which are well-known from the classical world, into the quantum realm.
It turns out that if you do it properly, you get some remarkable consequences, like a machine that both works and does not at the same time. These strange things arise (hardly surprising) from non-commuting observables in quantum mechanics.
Suppose we have a single atom, isolated from the outside world. For simplicity, let us assume that the consist of only two different energy levels. Then, we can easily identify its energy as the expectation value of its Hamiltonian. Nothing spectacular here. Now, we add an interaction with something else. Again, for simplicity, let's assume it is just some interaction with another atom. Now, this interaction will directly influence the atom and alter its energy levels. And, in general, due to entanglement with the other atom, the state the first atom can no longer be described by local properties alone.
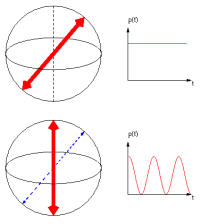 |
Depending on the
measurement base (red arrows), different dynamics of the excited
state is observed |
However, we still may perform measurements of the local energy, and ask ourselves whether one atom performs work on the other. And this is, where things are getting subtle. In thermodynamics, work is a process variable, and introducing the same idea into quantum mechanics results in a fixed measurement basis, in which we regard the situation. Obviously, there are many possible choices of this basis (infinitely many to be exact). Two possible choices are shown in the Bloch spheres on the right:
- The new energy eigenbasis: By definition, no transitions between the energy levels can be seen.
- The original energy eigenbasis: the interaction induces Rabi oscillations between the energy levels.
In case of no heat transfer, the work done on the atom is the change of its energy (this is simply the first law of thermodynamics). But in the first case there is no change in energy with respect to the measurement basis, while in the second case there is one. If we think of our atom as the working gas of a quantum thermodynamic machine we have a machine that both performs work and doesn't, depending on how you look on it.
As this example shows, the choice of the measurement basis is crucial. Which basis is appropriate depends on the context, i.e., how our atom is embedded into the rest of the outside world. And to honor the importance, we decided to give a catchy name to it: "Local Effective Measurement Basis", or shortly, "LEMBAS". Bon Appétit!
Reference: H. Weimer, M. J. Henrich, F. Rempp, H. Schröder,
G. Mahler. Local effective dynamics of quantum systems: A
generalized approach to work and
heat,
Europhys. Lett. 83, 30008
(2008).
arXiv:0708.2354
Copyright 2006--2011 Hendrik Weimer. This document is available under the terms of the GNU Free Documentation License. See the licensing terms for further details.